揭开这个神秘的面纱，探索其中的数学奥秘

BP神经网络概念

　　首先从名称中可以看出，BP神经网络可以分为两个部分，BP和神经网络。BP是Back Propagation的简写 ，意思是反向传播。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法也称为梯度下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

　　其主要的特点是：信号是正向传播的，而误差是反向传播的。

　　举一个例子，某厂商生产一种产品，投放到市场之后得到了消费者的反馈，根据消费者的反馈，厂商对产品进一步升级，优化，一直循环往复，直到实现最终目的——生产出让消费者更满意的产品。产品投放就是“信号前向传播”，消费者的反馈就是“误差反向传播”。这就是BP神经网络的核心。

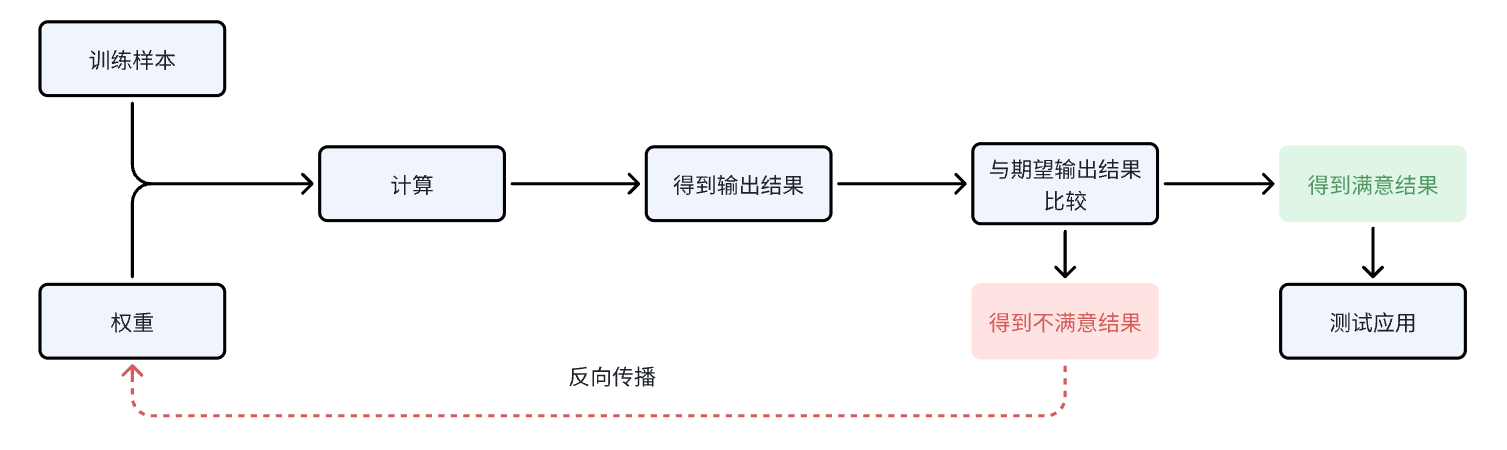
训练一个BP神经网络的核心步骤

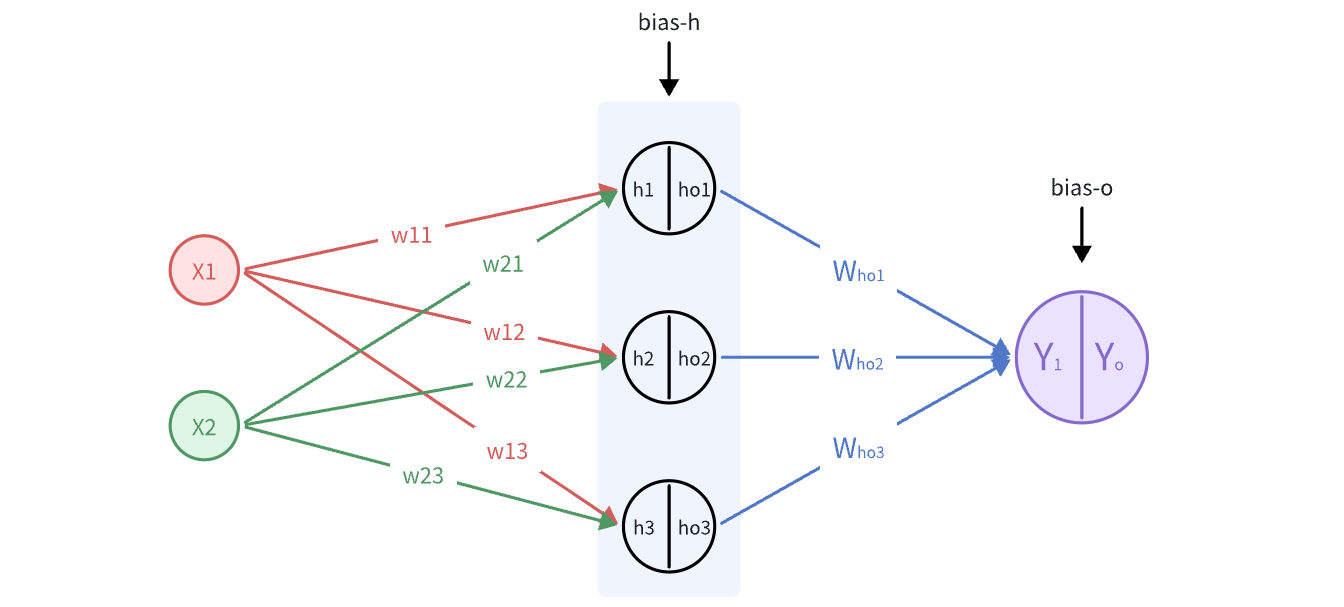
　　这张图基本反应了训练一个BP神经网络的核心步骤，很容易懂，不过多解释了。下面，我们以一个最简单的BP神经网络为例，来推导其计算过程。见下图：

前向传播

隐含层输入节点：

$$ \begin{aligned} h_{1}=W_{11}\cdot x_{1}+W_{21}\cdot x_{2}+b_{h1}\\ h_{2}=W_{12}\cdot x_{2}+W_{22}\cdot x_{2}+b_{h2}\\ h_{3}=W_{13}\cdot x_{3}+W_{23}\cdot x_{2}+b_{h3} \end{aligned} $$

隐含层输出节点：
经过激活函数$f\left( x\right) =\dfrac{1}{1+e^{-x}}$运算得到：

$$ \begin{aligned} h_{o1}=f\left( h_{1}\right) \\ h_{o2}=f\left( h_{2}\right) \\ h_{o3}=f\left( h_{3}\right) \\ \end{aligned} $$

这里提一点激活函数的导数，后面会用到：

$$ f^{'}(x)=\frac{0-(-e^{-x})}{(1+e^{-x})^{2}}=\frac{1}{1+e^{-x}}\times (1-\frac{1}{1+e^{-x}})=f(x)(1-f(x)) $$

输出层输入节点：

$$ \begin{aligned} y_{1}=W_{ho1}\cdot h_{o1}+W_{ho2}\cdot h_{o2}+W_{ho3}\cdot h_{o3}+b_{o} \end{aligned} $$

输出层输出节点：

$$ y_{o}=f\left( y_{1}\right) $$

反向传播

需要明白微积分中的链式法则，设$x$是实数，$f$和$g$是从实数映射到实数的函数。假设$y=g(x)$并且$z=f(g(x))=f(y)$。那么链式法则就是：

$$ \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx} $$

在算法中，会计算实际输出$y_{o}$和期望输出$d_{o}$的误差，如果这个误差大于设定的阈值，那么就会进行误差的反向传播。
定义损失函数：

$$ f_{error}=\dfrac{1}{2}\sum \left( d_{o}-y_{o}\right) ^{2} $$

损失函数中的$1/2$是为了后面求导计算方便而添加的。

🎯目标：更新$W$、$b$使$f_{error}$更小

输出层→隐藏层的更新

先看输出层，假设更新后的$b_{o}$为$b_{o}^{'}$，即$b_{o}^{'} = b_{o}+\Delta b_{o}$，只要求出$\Delta b_{o}$，就能得到$b_{o}^{'}$。
根据梯度下降的原则，可以知道：

$$ \Delta b_{o}=\eta \cdot \dfrac{\partial f_{error}}{\partial b_{o}} $$

根据上面的推导，可以知道：

$$ f_{error}=\dfrac{1}{2} \left( d_{o}-y_{o}\right) ^{2}=\dfrac{1}{2} (d_{o}-f(W_{ho1}\cdot h_{o1}+W_{ho2}\cdot h_{o2}+W_{ho3}\cdot h_{o3}+b_{o}))^2 $$

根据链式法则：

$$ \dfrac{\partial f_{error}}{\partial b_{o}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial b_{o}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial y_{1}}\cdot \dfrac{\partial y_{1}}{\partial b_{o}} $$

下面单独求解各个偏导：

$$ \dfrac{\partial f_{error}}{\partial y_{o}}=\dfrac{\partial (\dfrac{1}{2} \left( d_{o}-y_{o}\right) ^{2})}{\partial y_{o}}=-(d_{o}-y_{o}) $$

$$ \dfrac{\partial y_{o}}{\partial y_{1}}=\dfrac{\partial (\dfrac{1}{1+e^{-y_{1}}})}{\partial y_{1}}=y_{o}(1-y_{o}) $$

$$ \dfrac{\partial y_{1}}{\partial b_{o}}=\dfrac{\partial (W_{ho1}\cdot h_{o1}+W_{ho2}\cdot h_{o2}+W_{ho3}\cdot h_{o3}+b_{o})}{\partial b_{o}}=1 $$

所以：

$$ \dfrac{\partial f_{error}}{\partial b_{o}}=-(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o}) $$

所以：

$$ \Delta b_{o}=\eta \cdot \dfrac{\partial f_{error}}{\partial b_{o}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o}) $$

对于$W$，这里以$W_{ho1}$为例子，其他同理可得。
由链式法则：

$$ \dfrac{\partial f_{error}}{\partial W_{ho1}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial W_{ho1}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial y_{1}}\cdot \dfrac{\partial y_{1}}{\partial W_{ho1}} $$

式中的$\dfrac{\partial f_{error}}{\partial y_{o}}$和$\dfrac{\partial y_{o}}{\partial y_{1}}$已经计算过，无需再次计算。

$$ \dfrac{\partial y_{1}}{\partial W_{ho1}} = \dfrac{\partial (W_{ho1}\cdot h_{o1}+W_{ho2}\cdot h_{o2}+W_{ho3}\cdot h_{o3}+b_{o})}{\partial W_{ho1}}=h_{o1} $$

所以：

$$ \Delta W_{ho1}=\eta \cdot \dfrac{\partial f_{error}}{\partial W_{ho1}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot h_{o1} $$

这样就把输出层的$W$、$b$更新完成了，更新后的结果：

$$ b_{o}^{'} = b_{o}+\Delta b_{o}=b_{o}-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o}) $$

$$ \begin{aligned} W_{oh1}^{'} = W_{oh1}+\Delta W_{oh1}=W_{oh1}-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot h_{o1}\\ W_{oh2}^{'} = W_{oh1}+\Delta W_{oh2}=W_{oh2}-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot h_{o2}\\ W_{oh3}^{'} = W_{oh1}+\Delta W_{oh3}=W_{oh3}-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot h_{o3}\\ \end{aligned} $$

隐藏层→输入层的更新

这里以$b_{h1}$为例子。
此时：

$$ \begin{aligned} f_{\text{error}} &= \frac{1}{2} \left( d_{o} - y_{o} \right)^{2} \\ &= \frac{1}{2} \left( d_{o} - f \left( W_{ho1} \cdot f \left( x_{1} \cdot W_{11} + x_{2} \cdot W_{21} + b_{h1} \right) + W_{ho2} \cdot f \left( x_{1} \cdot W_{12} + x_{2} \cdot W_{22} + b_{h2} \right) \right. \right. \\ &\quad \left. \left. + W_{ho3} \cdot f \left( x_{1} \cdot W_{13} + x_{2} \cdot W_{23} + b_{h3} \right) + b_{o} \right) \right)^{2} \end{aligned} $$

由链式法则：

$$ \dfrac{\partial f_{error}}{\partial b_{h1}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial b_{h1}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial y_{1}}\cdot \dfrac{\partial y_{1}}{\partial h_{o1}}\cdot \dfrac{\partial h_{o1}}{\partial b_{h1}} $$

式中的$\dfrac{\partial f_{error}}{\partial y_{o}}$和$\dfrac{\partial y_{o}}{\partial y_{1}}$已经计算过，无需再次计算。

$$ \dfrac{\partial y_{1}}{\partial h_{o1}}=\dfrac{\partial (W_{ho1}\cdot h_{o1}+W_{ho2}\cdot h_{o2}+W_{ho3}\cdot h_{o3}+b_{o})}{\partial h_{o1}}=W_{ho1} $$

$$ \dfrac{\partial h_{o1}}{\partial b_{h1}}=\dfrac{\partial(f(W_{11}\cdot x_{1}+W_{21}\cdot x_{2}+b_{h1}))}{\partial b_{h1}}=h_{o1}(1-h_{o1}) $$

所以：

$$ \Delta b_{h1}=\eta \cdot \dfrac{\partial f_{error}}{\partial b_{h1}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho1} \cdot h_{o1}(1-h_{o1}) $$

同理，可以得到：

$$ \Delta b_{h2}=\eta \cdot \dfrac{\partial f_{error}}{\partial b_{h2}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho2} \cdot h_{o2}(1-h_{o2}) $$

$$ \Delta b_{h3}=\eta \cdot \dfrac{\partial f_{error}}{\partial b_{h3}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho3} \cdot h_{o2}(1-h_{o3}) $$

对于$W$，这里以$W_{11}$为例子，其他同理可得。
由链式法则：

$$ \dfrac{\partial f_{error}}{\partial W_{11}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial W_{ho1}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial h_{o1}}\cdot \dfrac{\partial h_{o1}}{\partial W_{11}}=\dfrac{\partial f_{error}}{\partial y_{o}}\cdot \dfrac{\partial y_{o}}{\partial y_{1}}\cdot\dfrac{\partial y_{1}}{\partial h_{o1}}\cdot \dfrac{\partial h_{o1}}{\partial W_{11}} $$

式中的$\dfrac{\partial f_{error}}{\partial y_{o}}$、$\dfrac{\partial y_{o}}{\partial y_{1}}$和$\dfrac{\partial y_{1}}{\partial h_{o1}}$已经计算过，无需再次计算。

$$ \dfrac{\partial h_{o1}}{\partial W_{11}}=\dfrac{\partial h_{o1}}{\partial h_{1}}\cdot \dfrac{\partial h_{1}}{\partial W_{11}}=h_{1}(1-h_{1})\cdot x_{1} $$

所以：

$$ \Delta W_{11}=\eta \cdot \dfrac{\partial f_{error}}{\partial W_{11}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho1} \cdot h_{1}(1-h_{1})\cdot x_{1} $$

同理，可以得到：

$$ \Delta W_{12}=\eta \cdot \dfrac{\partial f_{error}}{\partial W_{12}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho2} \cdot h_{2}(1-h_{2})\cdot x_{1} $$

$$ \Delta W_{13}=\eta \cdot \dfrac{\partial f_{error}}{\partial W_{13}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho3} \cdot h_{3}(1-h_{3})\cdot x_{1} $$

$$ \Delta W_{21}=\eta \cdot \dfrac{\partial f_{error}}{\partial W_{21}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho1} \cdot h_{1}(1-h_{1})\cdot x_{2} $$

$$ \Delta W_{22}=\eta \cdot \dfrac{\partial f_{error}}{\partial W_{22}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho2} \cdot h_{2}(1-h_{2})\cdot x_{2} $$

$$ \Delta W_{23}=\eta \cdot \dfrac{\partial f_{error}}{\partial W_{23}}=-\eta(d_{o}-y_{o})\cdot y_{o}\cdot (1-y_{o})\cdot W_{ho3} \cdot h_{3}(1-h_{3})\cdot x_{2} $$

这样就把输入层的$W$、$b$更新完成了。

下一篇开始手撕代码！